Равносильные логические выражения
Логические выражения, у которых последние столбцы таблиц истинности совпадают, называются равносильными. Для обозначения равносильных логических выражений используется знак "=". Докажем, что логические выражения ¬А ∧ ¬В и ¬(A ∨ B) равносильны. Построим сначала таблицу истинности логического выражения ¬А ∧ ¬В.
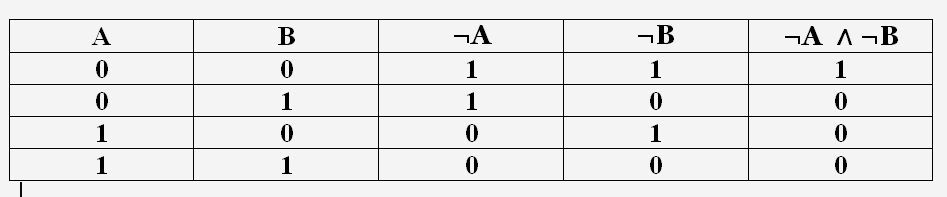
Теперь построим таблицу истинности логического выражения ¬(A ∨ B).

Значения в последних столбцах таблиц истинности совпадают, следовательно, логические выражения равносильны: ¬А ∧ ¬В = ¬(A ∨ B)
Логические функции
Логические функции
В обыденной и научной речи кроме базовых логических связок «и», «или», «не» используются и некоторые другие: «если... то...», «... тогда и только тогда, когда...» и др. Некоторые из них имеют свое название и свой символ, и им соответствуют определенные логические функции.
Логическое следование (импликация)
Логическое следование (импликация) образуется соединением двух высказываний в одно с помощью оборота речи «если..., то...». Логическая операция импликации «если А, то В», обозначается А → В.
Составное высказывание, образованное с помощью операции логического следования (импликации), ложно тогда и только тогда, когда из истинной предпосылки (первого высказывания) следует ложный вывод (второе высказывание).
Таблица истинности логической функции "импликации"
Например, высказывание "Если число делится на 10, то оно делится на 5" истинно, так как истинны и первое высказывание (предпосылка), и второе (вывод).
Высказывание "Если число делится на 10, то оно делится на 3" ложно, так как из истинной предпосылки делается ложный вывод.
Однако операция логического следования несколько отличается от обычного понимания слова «следует». Если первое высказывание (предпосылка) ложно, то вне зависимости от истинности или ложности второго высказывания (вывода) составное высказывание истинно. Это можно понимать таким образом, что из неверной предпосылки может следовать что угодно. В алгебре высказываний все логические функции могут быть сведены путем логических преобразований к трем базовым: логическому умножению, логическому сложению и логическому отрицанию. Докажем методом сравнения таблиц истинности, что операция импликации А → В равносильна логическому выражению ¬A ∨ B. Таблица истинности логического выражения ¬A ∨ B
КАРТИНКА
Высказывание "Если число делится на 10, то оно делится на 3" ложно, так как из истинной предпосылки делается ложный вывод.
Однако операция логического следования несколько отличается от обычного понимания слова «следует». Если первое высказывание (предпосылка) ложно, то вне зависимости от истинности или ложности второго высказывания (вывода) составное высказывание истинно. Это можно понимать таким образом, что из неверной предпосылки может следовать что угодно. В алгебре высказываний все логические функции могут быть сведены путем логических преобразований к трем базовым: логическому умножению, логическому сложению и логическому отрицанию. Докажем методом сравнения таблиц истинности, что операция импликации А → В равносильна логическому выражению ¬A ∨ B. Таблица истинности логического выражения ¬A ∨ B
КАРТИНКА
Таблицы истинности совпадают (т.е. значения в последних столбцах одинаковы), следовательно А → В = ¬A ∨ B. Логическое равенство (эквивалентность)
Логическое равенство (эквивалентность). Логическое равенство (эквивалентность) образуется соединением двух высказываний в одно с помощью оборота речи «... тогда и только тогда, когда ...» Логическая операция эквивалентности «А тогда и только тогда, когда В» обозначается А~В (или А ≡ В).
Составное высказывание, образованное с помощью логической операции эквивалентности истинно тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны. Таблица истинности логической функции эквивалентности
КАРТИНКА
Логическое равенство (эквивалентность). Логическое равенство (эквивалентность) образуется соединением двух высказываний в одно с помощью оборота речи «... тогда и только тогда, когда ...» Логическая операция эквивалентности «А тогда и только тогда, когда В» обозначается А~В (или А ≡ В).
Составное высказывание, образованное с помощью логической операции эквивалентности истинно тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны. Таблица истинности логической функции эквивалентности
КАРТИНКА
Рассмотрим, например, два высказывания: А="Компьютер может производить вычисления" и В="Компьютер включен". Составное высказываение, полученное с помощью операции эквивалентности, истинно, когда оба высказывания либо истинны, либо ложны: "Компьютер может проводить вычисления тогда и только тогда, когда компьютер включен". "Компьютер не может производить вычисления тогда и только тогда, когда компьютер не включен". Составное высказывание, полученное с помощью операции эквивалентности, ложно, когда одно высказывание истинно, а другое ложно: "Компьютер может производить вычисления тогда и только тогда, когда компьютер не включен". "Компьютер не может производить вычисления тогда и только тогда, когда компьютер включен". Докажем, используя таблицы истинности, что операция эквивалентности А~В равносильна логическому выражению: (A ∨ ¬B) ∧ (¬A ∨ B). Таблица истинности функции (A ∨ ¬B) ∧ (¬A ∨ B)
КАРТИНКА
Таблицы истинности совпадают (т.е. значения в последних столбцах одинаковы), следовательно А~В=(A ∨ ¬B) ∧ (¬A ∨ B).
